Өлшем
Өлшем (ағылш. dimension) – физика және математика ғылымдарында математикалық кеңістіктің (немесе объектінің) өлшемі деп ондағы әрқандай нүктені көрсету үшін шектеулі мөлшердегі қажетті координаттар саны айтылады.[1][2] Бір өлшем деп дененің бір қимасы айтылады. Мысалы, түзуде бір (1D) өлшем бар, өйткені ондағы нүктені көрсету үшін тек бір координат қажет болады. Цилиндрдің немесе шар секілді беттің өлшемі екі (2D) болады, себебі ондағы нүктені көрсету үшін екі координат қажет, яғни, беттегі нүктені айқындау үшін ендік және бойлық өлшемдері қажет. Екі өлшемді Евклидтік кеңістік — жазықтықтағы екі өлшемді кеңістік. Ал, кубтің, цилиндрдің немесе шардың ішкі жағы үш өлшемді (3D), себебі осы кеңістіктердегі нүктені табу үшін үш координат қажет.
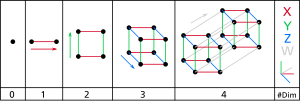

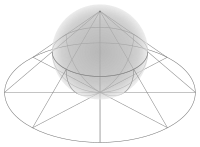
Классикалық механикада кеңістік пен уақыт ұқсамайтын категорияға жатады, әрі абсолютті кеңістік пен уақытқа байланысты. Ғалам ұғымы 4 өлшемді болып табылады, бірақ электромагнетизмді сипаттауға ол жарамайды. Уақыт-кеңістіктің төрт өлшемі (4D) кеңістіктік және уақыттық тұрғыдан абсолютті анықталмаған, қайта бақылаушы қозғалысына орай мәлім оқиғаларға сай анықталған. Минковский кеңістігі алғаш гравитациясыз ғаламды мөлшерлейді; жалпы салыстырмалы теорияның псевдо-римандық түрленісі (pseudo-Riemannian manifolds) уақыт-кеңістікті материямен және гравитациямен сипаттайды. 10 өлшемділік суперструна теориясын (6D гиперкеңістік + 4D) сипаттау үшін пайдаланылады; ал 11 өлшемділік супергравитация мен М-теориясын (7D гиперкеңістік + 4D) сипаттай алады; ал кванттық механиканың күй кеңістігі шексіз өлшемді функция кеңістігін білдіреді.
Өлшем ұғымы физикалық нысандармен шектелмейді. Жоғары өлшемді кеңістіктер математика мен ғылымда жиі кездеседі. Олар евклидтік кеңістіктер немесе жалпы параметрлік кеңістіктер немесе Лагранж немесе Гамильтон механикасындағы секілді конфигурациялық кеңістіктер болуы мүмкін; бұлар физикалық кеңістікке тәуелсіз абстрактілі кеңістіктер.
Философияда өлшем көбінесе нәрседегі сан-сапа бірлігі мен қайшылығының ең жинақы стандартын білдіреді. Гегель диалектикасында өлшем сан-сапа өзгерісіндегі сандық және сапалық күйдің түрлі деңгейлерін бідіреді. Ол бойынша, сапа мен сан арасында терең байланыс бар. Өзгеріс сандық өлшемдердің өзгерісінен басталып, мәлім шекке жеткенде сапалық өлшемдердің өзгерісіне ауысады, сөйтіп зат өзінің жаңа нұсқасына ауысады. Сондықтан Гегель өлшемді “сандық сапа” немесе “сапалық сан”, яғни сапа мен санның бірлігі деп анықтаған.[3]
Дереккөздер
өңдеу- ↑ Curious About Astronomy. Curious.astro.cornell.edu.
- ↑ MathWorld: Dimension. Mathworld.wolfram.com (27 ақпан 2014).
- ↑ Қазақ тілі терминдерінің салалық ғылыми түсіндірме сөздігі. — Алматы: "Мектеп" баспасы, 2007. ISBN 9965-36-417-6