Архимед заңы

Архимед заңы – аэростатика мен гидростатиканың сұйыққа (газға) батырылған денеге, көлемі сол дененің көлеміндей сұйықтың салмағына тең әрі одан әрқашан да жоғары қарай бағытталған кері итеруші күш әсер ететіндігін анықтайтын негізгі заңы. Дененің ығыстырып шығарған сұйығының ауырлық центріне (орталығына) түсетін итеруші күшті архимедтік не гидростатикалық көтеруші күш деп атайды. Егер дененің салмағы архимедтік күштен кем болса, онда дене сұйық бетіне қалқып шығады, ал дененің салмағы архимедтік күштен артық болса, онда дене сұйыққа батып кетеді. Дененің салмағы архимедтік күшке тең болса, дене сұйық ішінде жүзіп жүреді. Бұл заңды Архимед б.з.б. 3 ғасырда ашқан. Архимед заңы денелердің сұйықта, не газда жүзуінің теориялық негізі болып саналады.

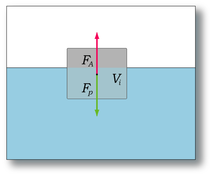
Архимед күші өңдеу

Архимед күші — тепе-теңдік жағдайдағы сұйыққа тұтастай немесе жартылай батырылған кез келген дененің бетіне төменнен жоғарыға қарай тік бағытта әсер ететін гидростатикалық қысым күші. Архимед күші ауырлық күшіне қарсы бағытталған. Тік жоғары бағытталған көтеруші күш (Архимед күші) көлемі дене көлеміндей сұйық салмағына тең болады: Р = gV = G; G - дененің салынған ортаның тығыздығы, V — дененің көлемі. Дененің салмағы мен көтеруші күштің шамаларын салыстырып, дененің сұйық ішіндегі тепе-теңдік жағдайын анықтауға болады. Егер: Р < G болса, онда дене сұйықтыққа батып кетеді. Р > G жағдайында дене сұйық бетіне қалқып шығады, ал Р = G кезінде дене сұйық ішінде жүзіп жүреді.^[1]

Формуласы : Fa=pc*Vд*g , яғни Архимед күші тең болады сұйықтық тығыздығының, дене көлемінің және еркін түсу үдеуінің көбейтіндісіне.

Архимед күші жайлы аңыз өңдеу

Аңызда айтылатындай, Сиракуз патшасы Гиерон Архимедке зергер жасаған тәждің таза алтыннан немесе алтын мен күмістің қоспасынан жасалынғанын анықтауды тапсырды. Бұл есепті шеше алмай, Архимед көп күн әуреленді. Бір күні толтыра су құйылған ваннаға түскен кезде кенеттен ойына әлгі есептің шешуі келген екен дейді. Өзінің ашқан жаңалығына шаттана куанған ол «Эврика!» (Таптым!) деп Сиракуз көшелерінің бойымен айғайлап жүгірген екен. Сірә, жаңалық ашқан адам ерекше бір сезімге бөленетін болар.

1-тәжірибе өңдеу

A.

1-сурет.

Архимедтің ашқан жаңалығының мән-мағынасын түсіну үшін қарапайым тәжірибе жасап көрейік. Динамометр ілгегіне қандай да бір дене ілейік те, оның шкаласының көрсетуі бойынша ауырлық күшінің мәнін белгілеп алайық (1, а-сурет). Осыдан кейін денені толық суға батырайық (1, ә-сурет). Динамометр көрсетуі өзгергенін байқаймыз. Неліктен? Дененің массасын өзгерткеніміз жоқ. Демек, бұл жағдайда денеге ауырлық күшінен басқа оны судан ығыстыратын күш әрекет етеді. Ол күш қалай пайда болады? Сұйықтың қысымы туралы білімімізге сүйене отырып, осы сұйыққа батырылған денеге қандай күштер әрекет ететінін қарастырайық. Дененің бүйір жақтарына әрекет ететін күштер тең және олар бірін-бірі теңгеріп тұрады. Бұл күштердің әрекетінен дене тек сығылады. Дененің үстіңгі жағын биіктігі һ1 су бағаны F1 күшпен, ал төменгі жағын биіктігі һ2 су бағаны F2 күшпен қысады. Мұндағы һ2, су бағанының биіктігі һ1 биіктіктен көп, сондықтан F2 күші де F1 күштен көп болады. Демек, денені сұйықтан ығыстыратын күш F1 және F2 күштерінің айырымына тең, яғни

F = F2 - F1

Сонымен, сұйыққа батырылған денеге осы денені сұйықтан ығыстыратын күш әрекет етеді.

2-тәжірибе өңдеу

Енді биіктігі һ табанының ауданы S болатын параллелепипед тәрізді денеге тығыздығы ρ_с сұйық тарапынан әрекет ететін ығыстырушы күштің мәнін анықтайық. Алдымен дененің үстіңгі бөлігіне сұйықтың түсіретін қысым күшін есептейік. h₁ сұйық бағанының дененің үстіңгі бетіне түсіретін қысымы

p₁ = ρ_сg h₁ онда

F₁ = p₁S = ρ_сg h₁S

болады. Ал дененің төменгі бетіне сұйықтың түсіретін қысым күші:

F₂ = p₂S = ρ_сg h₂S, мұндағы

p₂ = ρ_сg h₂ - биіктігі h₂ сұйық бағанының қысымы.

Онда F_ы = F₂ - F₁ = ρ_сg (h₂ - h₁)S

Параллелипипед биіктігі һ(һ= h₂ - h₁) екенін ескерсек, онда

F_ы = ρ_сghS немесе F_ы= ρ_сgV_д

болады, мұндағы V_д=Sh – дененің көлемі.

Ығыстырушы күштің формуласына сұйықтың тығыздығы кіретініне назар аударайық. Ал бұдан дене көлемінің сұйық тығыздығына көбейтіндісі дененің алатын көлеміндегі сұйық массасын береді: m_с = ρ_с V_д Егер дене сұйыққа толық батпаған болса, онда ρ_с V_д көбейтіндісі дененің сұйыққа батқан бөлігі алатын көлеміндегі сұйық массасын береді, яғни F_ы= ρ_сgV_б.б. , мұндағы V_б.б. – дененің сұйыққа батқан бөлігінің көлемі. Бұл өрнектің оң жағы сұйыққа батырылған дене ығыстырған сұйықтың салмағына тең екенін байқауға болады.

3-тәжірибе өңдеу

A.

2-сурет.

Ығыстырушы күштің мәнін біз теориялық түрде қорытып шығардық. Енді алынған нәтижені тәжірибеде тексерейік. Динамометр ілгегіне цилиндр тәрізді дене және осы дене ішіне толық сыятындай ыдыс ілейік (2, а-сурет). Осыдан кейін денені суға батырғанға дейінгі динамометр көрсетуін белгілеп алайық. Үстелге шүмегінің деңгейіне дейін су құйылған ыдыс және оның қасына кішірек сауыт қояйық. Енді денені абайлап ыдыстағы суға батырамыз. Ығыстырушы күштің әрекетінен динамометр серіппесінің көрсеткіші жоғары көтеріле бастайды. Дене суға батқан сайын суды ығыстыра түседі де, ығыстырылған су сауытка құйылады. Дене суға толық батқан кезде, динамометр дененің судағы салмағы қаншаға азайғанын көрсетеді (2,ә-сурет). Егер дене ығыстырып шығарған сүйықты динамометрге ілінген ыдысқа құйсақ, онда динамометр көрсеткіші өзінің бұрынғы орнына қайтадан келеді (2,б-сурет). Бұдан дененің салмағы ыдыстан ағып шыққан сұйықтың салмағына тең шамаға азайғанын байқаймыз. Осы байланысты Архимед те байқаған болатын. Енді Архимед заңын тұжырымдайық: сұйыққа батырылған денеге оның сұйыққа батқан бөлігі көлеміндегі сұйықтың салмағына тең ығыстырушы күш әрекет етеді. Сұйыққа батырылған денені ығыстыратын F_ы күшті архимед күші (F_а) деп те атайды. Сонымен:

F_а = ρ_сgV_д

Архимед күші сұйыққа батырылған дененің тығыздығына тәуелді болмайтынына көңіл аударыңдар. Архимед заңын тұжырымдауда біз «салмақ» сөзін қолдандық. Салмақ дегеніміз - дененін тірекке әрекет ететін күші екенін есімізге түсірейік. Тірек жерге қатысты козғалмайтын болса, онда дененің салмағы өзінің сан мәні жағынан ауырлық күшіне тен болады. Біз «салмақ» ұғымын салмақ пен ауырлық күшінің сан мәндері бір-біріне тең болатын жағдайлар үшін қолдандық және қолданатын боламыз. Ауадағы немесе кез келген газдағы денеге де ығыстырушы күш әрекет етеді. Егер біз бір денені газға батырып, жоғарыдағыдай тәжірибе жасаған болсақ, онда газ ішіндегі денені ығыстыратын күш сол дене ығыстырған газдың салмағына тең болатындығын байқаймыз. Бұл күш денеге әрекет ететін ауырлық күшінен едәуір аз болғандықтан, оны байқау да қиын. Алайда осы ығыстырушы күш есебінен ауа шарлары, дирижабльдер жоғары көтеріледі.

4-тәжірибе өңдеу

Пішіні күрделі немесе үлкендеу денелердің тығыздығын Архимед заңына негізделген гидростатикалық өлшеу әдісі арқылы анықтауға болады. Алдымен дененің салмағы ауада өлшенеді. Осыдан кейін дене тығыздығы белгілі сұйыққа толық батырылады. Денеге әрекет ететін екі күш бұл жағдайда тең және қарама-қарсы бағытталғандықтан (ауырлық күші төмен қарай, ал архимед күші жоғары қарай), дененің сұйық ішіндегі Р1 салмағы дененің ауадағы Р = mg салмағынан F_а=pg V_д архимед күшіне тең шамаға кем болады, яғни Р₁=Р - F_а , ал бұдан сұйыққа толық батырылған денеге әрекет ететін архимед күші F_а=Р- Р₁ немесе ρ_сgV_ы.с. = Р- Р₁

мұндағы V_ы.с. - дене ығыстырған сұйықтың немесе газдың көлемі. Егер дене сұйыққа толық бататын болса, онда ығыстырылған сұйықтың көлемі дененің көлеміне (V_д= V_ы.с.) тең болады. Дененің салмағы Р= ρ_дgV_д екенін ескерсек, онда

V_{d}={{P} \over {g\rho _{d}}}

мұндағы ρ_д- дененің тығыздығы. Түрлендіруден кейін

{P-P_{1}}={{P} \over {g\rho _{d}}}g\rho _{c}

аламыз, ал бұдан дененің тығыздығы:

\rho _{d}={{P} \over {P-P_{1}}}\rho _{c}

болады.^[2]

Дененің жүзу шарттары өңдеу

Сұйықтықта немесе газда орналасқан дененің жүзуі, немесе батуы оның ауырлық күші $\mathbf {F} _{P}$ мен Архимед күштерінің $\mathbf {F} _{A}$ модульдерінің қатынасымен анықталады. Әр бір дене үшін келесі үш жағдай болуы мүмкін:

$\mathbf {F_{P}} >\mathbf {F} _{A}$ — дене батады;
$\mathbf {F_{P}} =\mathbf {F} _{A}$ — дене сұйықтықта немесе газда жүзеді;
$\mathbf {F_{P}} <\mathbf {F} _{A}$ — дене жүзбейінше қалқып шыға береді.

Басқа формулировка (мұнда $\mathbf {p_{d}}$ — дене тығыздығы, $\mathbf {p_{o}}$ — дене батырылған ортаның тығыздығы):

$\mathbf {p_{d}} >\mathbf {p} _{o}$ — дене батады;
$\mathbf {p_{d}} =\mathbf {p} _{o}$ — дене сұйықтықта немесе газда жүзеді;
$\mathbf {p_{d}} <\mathbf {p} _{o}$ — дене жүзбейінше қалқып шыға береді.

Дереккөздер өңдеу

↑ Қазақ тілі терминдерінің салалық ғылыми түсіндірме сөздігі. Су шарушылығы. – Алматы, «Мектеп» баспасы, 2002 жыл.
↑ Физика және астрономия. - Алматы: Атамұра,2007.ISBN 9965-34-634-8

Бұл — физика бойынша мақаланың бастамасы. Бұл мақаланы толықтырып, дамыту арқылы, Уикипедияға көмектесе аласыз.

[1] Қазақ тілі терминдерінің салалық ғылыми түсіндірме сөздігі. Су шарушылығы. – Алматы, «Мектеп» баспасы, 2002 жыл.

[2] Физика және астрономия. - Алматы: Атамұра,2007.ISBN 9965-34-634-8

[1]

[2]